
(Photo by Annie Spratt on Unsplash)
在通过月平息计算实际年利率一文,计算实际年利率(APR)过程中,我发现了三个特点。
1、APR的多少与贷款金额没有关系,给定月平息利率和贷款期限,就可以把APR算出来。
2、给定月平息利率后,并不是贷款期限越长,APR就越大,贷款期限与APR存在一个非线性关系。
3、给定贷款期限后,APR会随月平息利率增大而增大,它们也呈现出非线性关系。
固定年平息利率为2.5%,查看APR与贷款期限的关系
当固定年平息利率为2.5%时,即月平息利率为0.2083%,贷款期限从6个月到360个月,APR取值如下图所示。
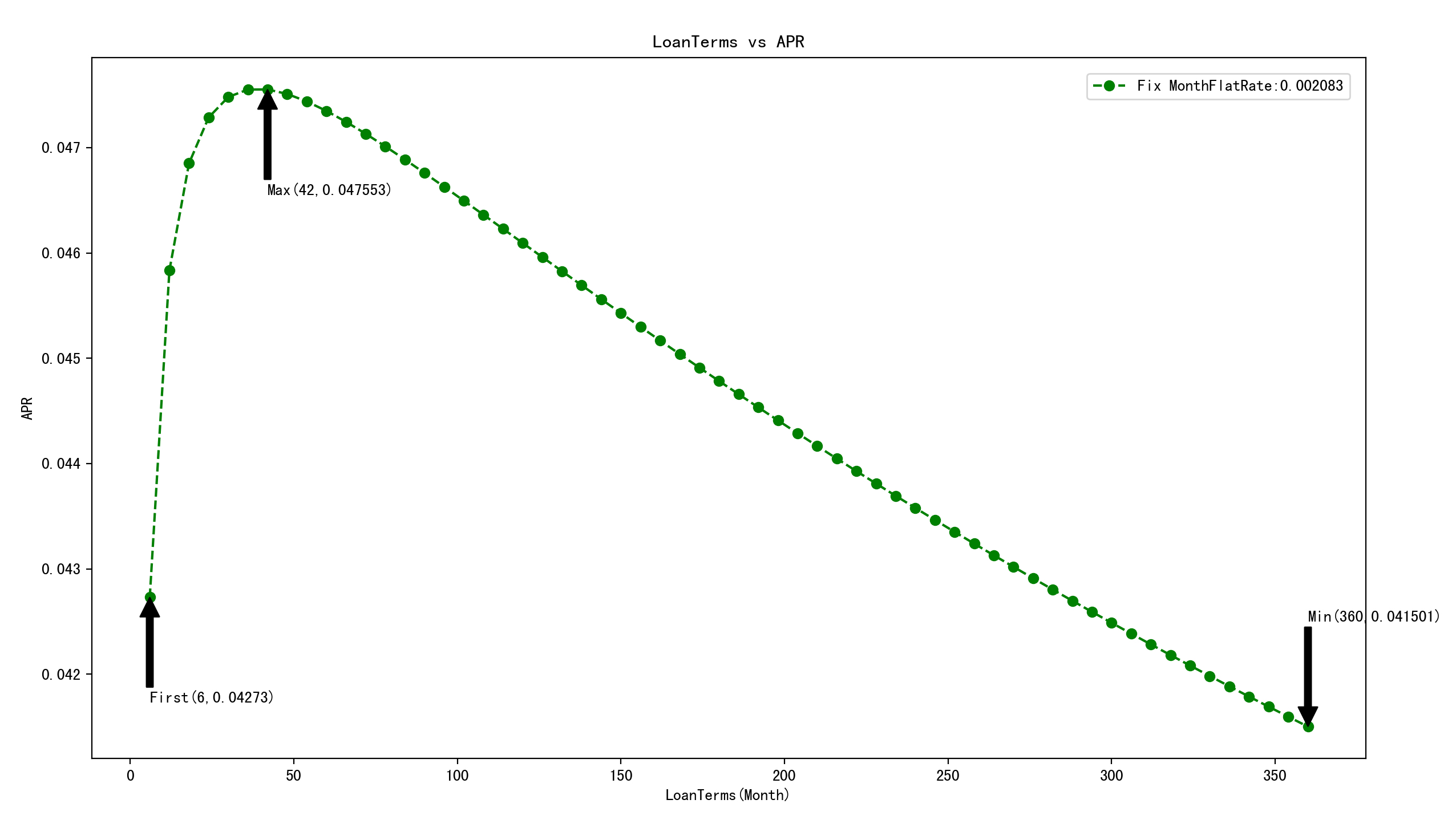
(横坐标:贷款期限;纵坐标:实际年利率APR)
第一个取值,APR最大那个值,APR最小那个值分别如下,也就是图中箭头标注的地方。
|
|
我们发现:
1.贷款期限从6个月增加到42个月过程中,APR会逐渐增大;
2.贷款期限等于42个月时,APR达到极大值,等于0.047553;
3.贷款期限从42个月增加到360个月过程中,APR逐渐减小;
4.贷款期限等于360个月时,APR达到极小值,等于0.041501;
固定年平息利率为4.8%,查看APR与贷款期限的关系
当固定年平息利率为4.8%时,即月平息利率为0.4%,贷款期限从6个月到360个月,APR取值如下图所示。
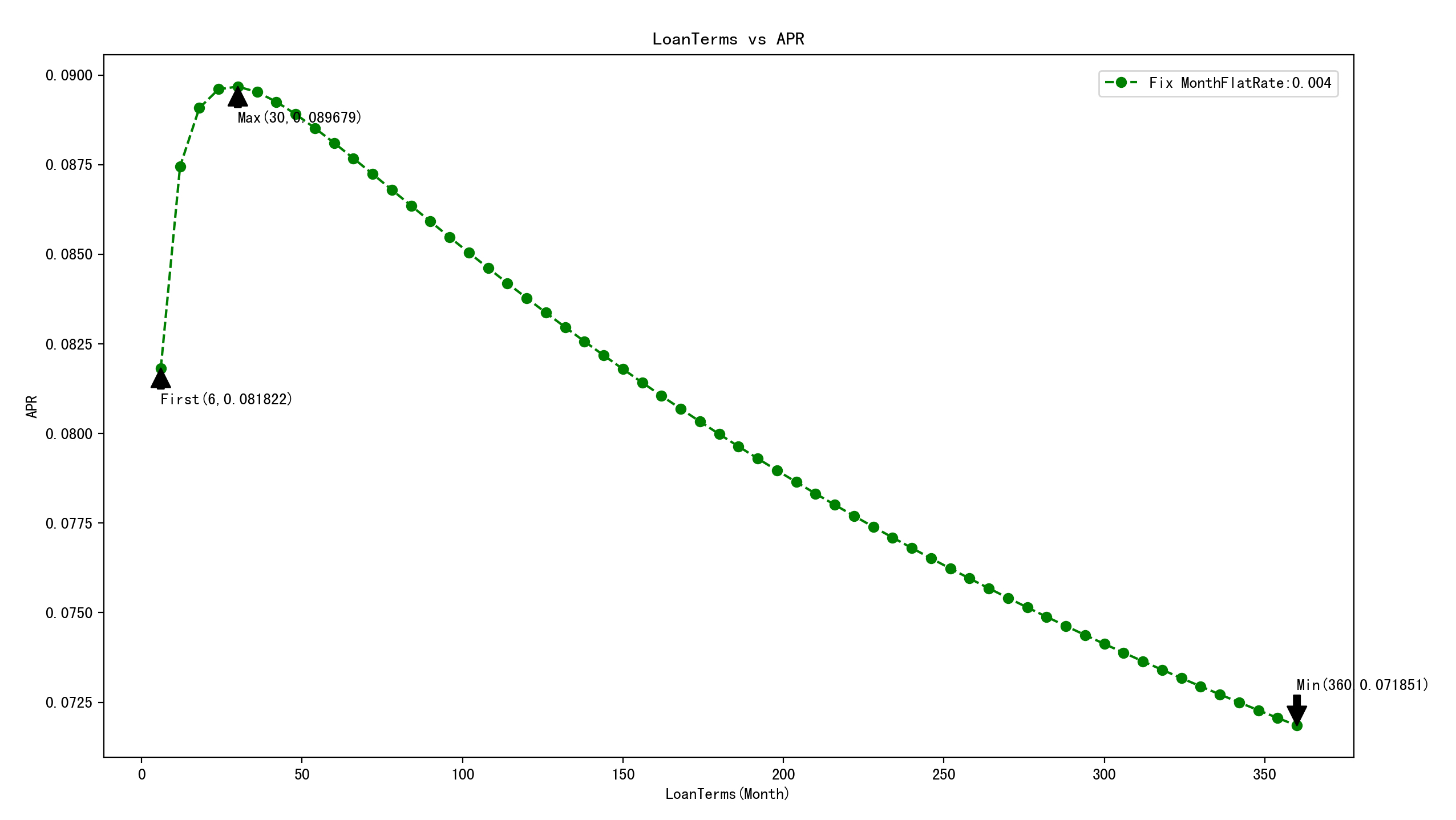
(横坐标:贷款期限;纵坐标:实际年利率APR)
第一个取值,APR最大那个值,APR最小那个值分别如下,也就是图中箭头标注的地方。
|
|
我们发现:
1.贷款期限从6个月增加到30个月过程中,APR会逐渐增大;
2.贷款期限等于30个月时,APR达到极大值,等于0.089679;
3.贷款期限从30个月增加到360个月过程中,APR逐渐减小;
4.贷款期限等于360个月时,APR达到极小值,等于0.071851;
5.年平息利率增加后,APR取极大值的位置提前了;(年平息4.8%时,30期时APR最大;年平息2.5%时,42期最大);
几乎可以肯定的是,如果贷款期限继续增大,APR还会继续减小,但一般来说,贷款的年期很少会超过30年,我们就不去进行后面的计算了。不过,我认为,即使APR继续减小,但它也是有一个极限值,这个极限值是多少,哪天有空我们再来推算它。
固定贷款期限为12个月,查看APR与月平息利率的关系
当固定贷款期限为12个月时,月平息利率从0.0833%到1%(即年平息利率从1%到12%),APR取值如下图所示。
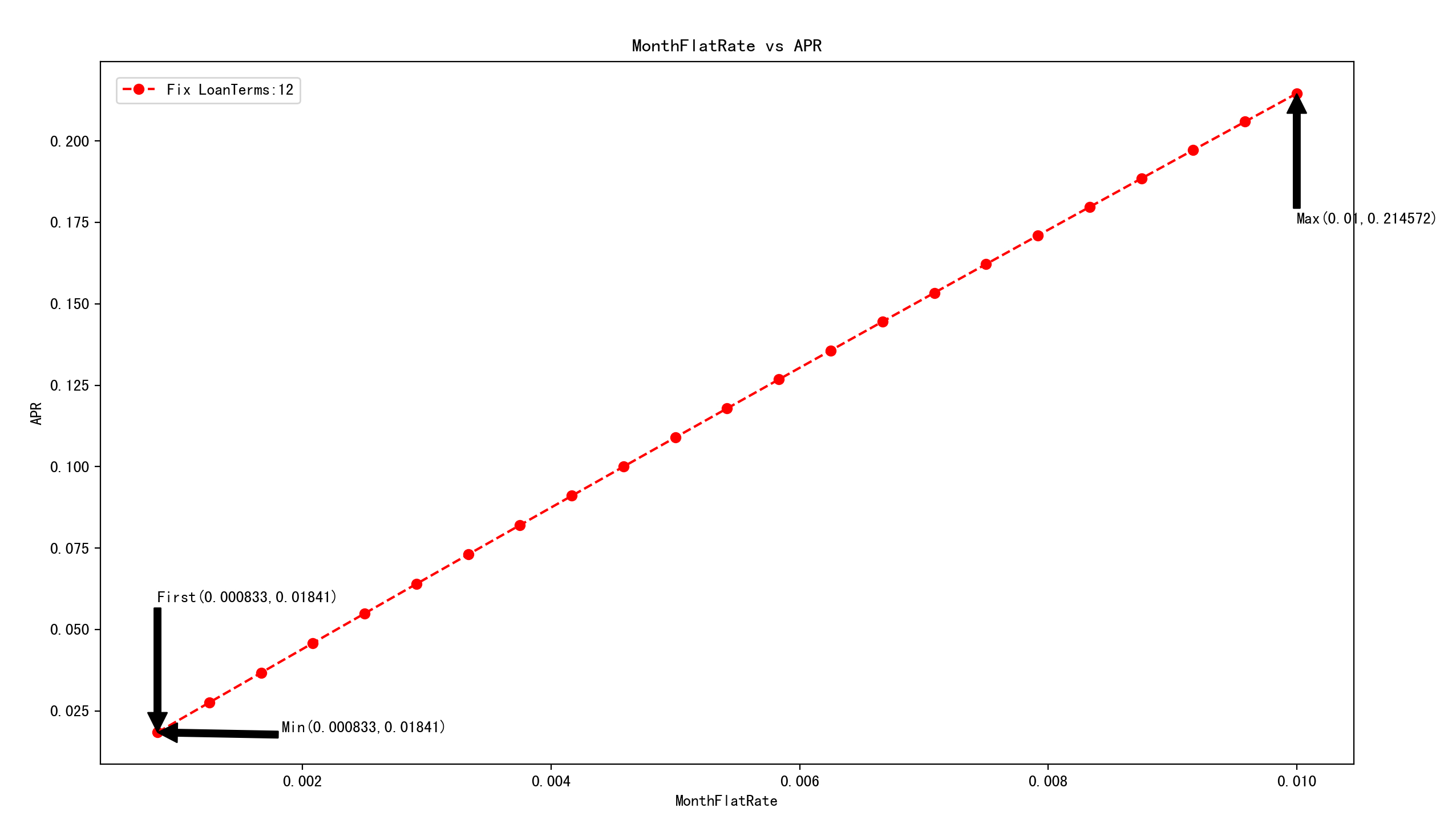
(横坐标:月平息利率;纵坐标:实际年利率APR)
第一个取值,APR最大那个值,APR最小那个值分别如下,也就是图中箭头标注的地方。
|
|
我们发现:
1.月平息利率从0.0833%增加到1%过程中,APR会逐渐增大;
2.APR与月平息利率的比值,第一期为0.01841/0.000833=22.1008,最后一期为0.214572/0.01=21.4572;
3.APR与月平息利率的比值逐渐减小;
4.APR与月平息利率看图形感觉像是线性关系,但实际是非线性关系;
固定贷款期限为48个月,查看APR与月平息利率的关系
当固定贷款期限为48个月时,月平息利率从0.0833%到1%(即年平息利率从1%到12%),APR取值如下图所示。
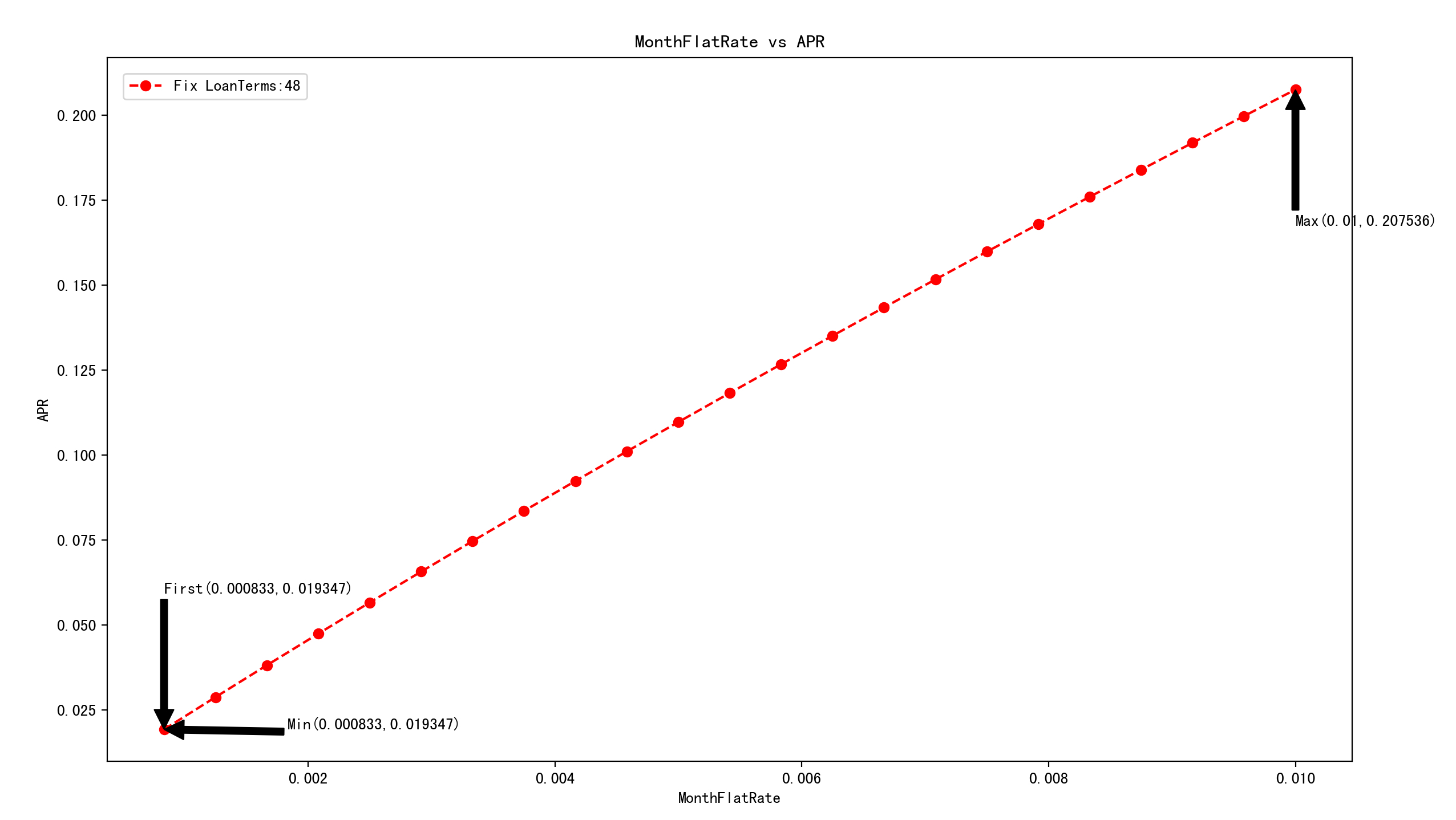
(横坐标:月平息利率;纵坐标:实际年利率APR)
第一个取值,APR最大那个值,APR最小那个值分别如下,也就是图中箭头标注的地方。
|
|
我们发现:
1.月平息利率从0.0833%增加到1%过程中,APR会逐渐增大;
2.APR与月平息利率的比值,第一期为0.019347/0.000833=23.22569028,最后
一期为0.207536/0.01=20.7536;
3.APR与月平息利率的比值逐渐减小;
4.APR与月平息利率看图形感觉像是线性关系,但实际是非线性关系;
5.APR与月平息利率的比值在一个常数附件波动,因此有”将月平息乘以常数21.5就近似得到APR的值“这一说法;
可以推测的是,如果月平息利率继续增大,APR会随之继续增大,APR与月平息利率的比值将会继续减小;由于金融机构发放贷款的利率严格受到政府监管,上述计算中,月平息利率上限我使用了1%,这个值已经很大了;再大就显得不太现实,过高的利率,监管机构是不会准许的,客户也不会傻到以这么高的利率来借钱。
但从数学计算的角度,即便月平息利率真的可以无限大,我觉得APR最终也会达到一个极限值,无法再增加下去。
